多模式模糊匹配
最近遇到一个字符串匹配的问题,给定多个由星号(*)作为通配符的模式串,用什么方法能尽可能快地找到那些模式串匹配成功。
譬如,下面三个模式串:
a*x*z
ab*z
abc*
目标串abxyz只能匹配其中第1,2个模式串。
当前的方法
现在正在使用的方法是一种简单的循环匹配的方法。在一个循环里面,依次用模式串匹配目标串,如果匹配成功则标记,最后输出所有匹配成功的模式串。
对于每个模式串和目标串的匹配,我们采用了一种ARN的方法(算法名称有待确认),递归地搜索可能的匹配。下面这张图展示了模式串a*bc对目标串ababc的匹配搜索过程。
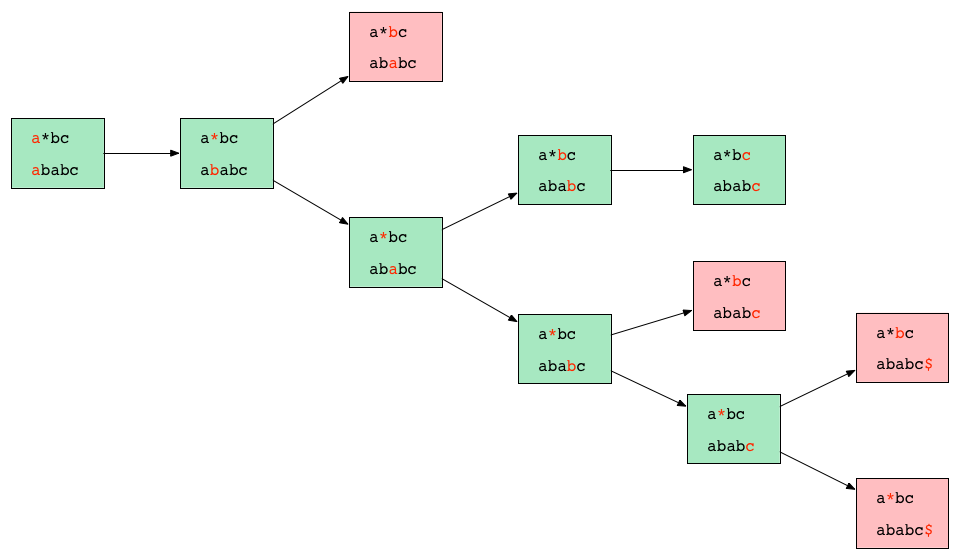
这种算法的时间复杂度计算起来有点复杂,不妨假设m为一个模式串与目标串匹配的平均时间,那么算法的时间复杂度就为O(mn),其中n为模式串的数量。简单地讲,就是算法时间与模式串的数量成线性正比例关系。
探索DFA
上面提到的算法,O(mn)的复杂度意味着模式串的数量会影响引擎的执行时间。而在我们的使用场景中,模式串的数量一般会成批量的出现。于是我们开始尝试探索一种一次匹配便能得到全部结果的方法。
AC自动机是一种高效的多模式匹配算法,但是它不适合我们。因为,第一,它只针对纯文本,不支持模糊匹配;第二,它的性能体现在对大目标文本串的匹配,因为有“滑动”所以避免了回溯,而我们的目标串一般是比较小的。
正则表达式 第一次尝试
后来,我想到了这种多模式模糊匹配其实可以转换成单个正则表达式来进行。
譬如,文章开头提到的那3个模糊串可以用下面的正则表达式来等效代替:
^a.*x.*z$|^ab.*z$|^abc.*$
用这种方法只能知道是否有模式被匹配,但不能知道是哪个模式被匹配到。不过好在正则表达式提供了捕获。用圆括号把每个模式串捕获,匹配成功的时候能通过捕获的matchid知道是哪个模式串匹配成功。
(^a.*x.*z$)|(^ab.*z$)|(^abc.*$)
用Linux下pcre自带的pcretest程序测试一下这种方法:
$ pcretest
PCRE version 8.35 2014-04-04
re> /(^a.*x.*z$)|(^ab.*z$)|(^abc.*$)/
data> abxyz
0: abxyz
1: abxyz
可以看到编号为1的捕获被输出了,证明这种方法可行。
用这种方法同前面那种循环匹配的方法对比测试,结果是在模式串数量大于5的情况下,正则的性能远远好于那种方法,而且随着模式串的数量增加,正则的性能相对稳定。而循环匹配的方法则直线下降。
但是,等等。。仔细想想,上面那个例子应该是前两个模式都能match,为何只有1号捕获被输出了?注意0号捕获代表的时整个串,不能考虑在内。
想想可能是因为pcre在匹配的时候,如果发现一个分支匹配成功,便会放弃其他分支而退出。也就意味着直接基于正则表达式的路子走不通。
自己扩展正则的功能
虽然直接基于标准正则表达式的路子没走通,但至少正则表达式的性能被证明是更优秀。那问题就是,能不能扩展一下现有的正则,使之能走完全部的分支并且标记哪些分支是匹配成功的?
看了下pcre的源代码,短时间看懂都比较困难,更别说改了,所以就暂时不考虑修改pcre了。《编译原理》这本书告诉我们,正则表达式的内部其实是一个NFA/DFA的自动机。看了一下书上的讲解,感觉也不是很复杂,然后又到网上搜了一个大神在1969年写的DFA正则的C语言实现(里面有源代码)。
于是,我把那个DFA的自动机修改了一下,转为直接支持星号(*)通配符匹配,同时增加了一个标记功能。这个标记功能是这样的,它是一个特殊的带有id的状态,如果自动机匹配到这里,就会被直接传送到终结状态,并记录匹配的模式串ID。同时,DFA有个特点就是能够输出所有match到的分支。所以,通过这种方式的扩展,一个能自动标记的多模式模糊匹配引擎就诞生了。
(TODO: 源码上传)
下面图表中的红线代表循环匹配的算法的执行时间,绿线代表基于DFA匹配的算法的执行时间,横轴是模式组的数量。
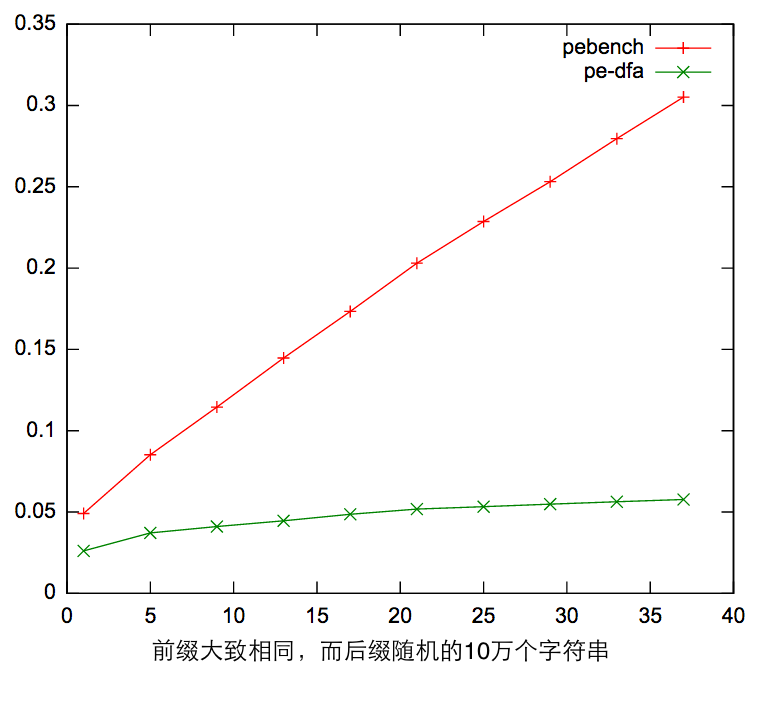
峰回路转:PCRE callout
虽然自己实现的DFA引擎表现不错,但是心中总是隐隐觉得一定有专门解决这个问题的项目,只是我没有发现它而已。 怀着这样的心态,我在网上搜了一圈,主要是以“多模式”、“模糊”和“匹配”等关键字进行搜索。搜索很像寻宝,一开始都是盲目地搜索,只要一点线索出现,你就会顺着这点线索顺藤摸瓜,找到更多线索,最后连根拔起。虽然记不得过程是怎样的了,但最终我找到了PCRE callout这个奇葩,能解我的问题。
废话不多说,先来看看PCRE callout是什么东西?
PCRE callout是一种在匹配过程中将控制权临时转交给调用者的功能。调用者提供一个callback函数,并将这个callback函数赋值给全局变量pcre_callout。在正则表达式中,一旦到达(?C)即会触发这个这个callback函数。不同的callout点可以设置不同的ID,这个ID是一个小于256的整数。例如,这个pattern包含两个callout点:
(?C1)abc(?C2)def
基于callout,我们可以这样实现多模式匹配:在每个模式串的末尾添加一个callout点,每个callout带一个唯一的ID,当一个模式匹配时,相应的callout点就会被触发,在callout的函数中,记录下是哪一个模式串匹配。
PCRE提供了两个exec函数:pcre_exec和pcre_dfa_exec。如果存在多条分支,pcre_exec会在第一条分支匹配成功之后结束,而pcre_dfa_exec则会走完所有可能的分支。man pcreapi对pcre_dfa_exec是这样介绍的:
第二种匹配函数,pcre_dfa_exec()不是Perl兼容的。它使用了一种不同的匹配算法——Alternative算法,这种算法会寻找所有可能的匹配,并且只需要扫描目标串一次。但是,这种算法不能返回捕获(captured substrings)。
所以,在我们的使用场景中,只能调用pcre_dfa_exec。
总结
在这次研究中,我有机会学习了《编译原理》中的NFA和DFA自动机,并且对DFA正则表达式引擎的原理有了一定的了解,并且亲自将一个简单的DFA正则表达式改造成了通配符的模式。最重要的是发现了PCRE callout这个重要的feature。